統計学基礎

平均 \( \bar{x} \)

\( \huge \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i}\)

\(x_{i}\)をiの1からn番目までを全て足し合わせて、\(n\)個で割ること

分散 \( s^2\)

\( \huge s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{i} – \bar{x})^2 \)

平均からの差（偏差）をiの1からn番目までを全て足し合わせ、\(n \)個で割ること

標準偏差 \(s \)

\( \huge s = \sqrt {s^2} \)

分散の平方根

標準化得点 \(z \)

\( \huge \frac{x_{i} – \bar{x}}{s}\)

変数の値から平均を引いて、標準偏差で割ること。

平均を0に、ばらつきを標準偏差1で統一する

変動係数 \( cv \)

\( \huge \frac{s}{\bar x} \)

標準偏差を平均で割る。

異なる変数間を比較しやすくなる。

四分位数

最小値

第1四分位数：下から25%区切りの値

第2四分位数（中央値）：真ん中の値。偶数の場合は二つの値の平均

第3四分位数：下から75%区切りの値

最大値

四分位範囲：第1四分位数から第3四分位数の間

箱ひげ図

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,20,30までの値を箱ひげ図で表現すると以下のようになる。

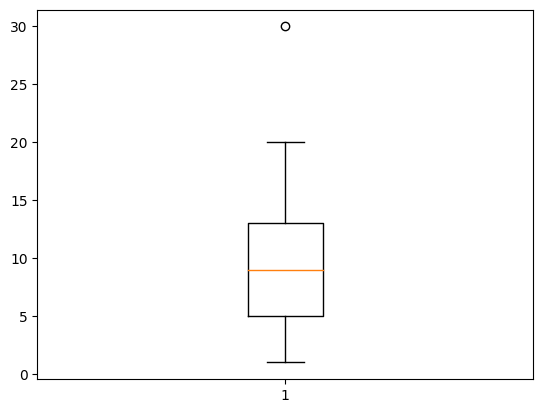
1-15までの間のちょうど真ん中である10が黄色の線で表される。

30は外れ値になるため、箱の中には入りきらず、丸で表現される。

範囲は、最大値から最小値を引くことで求められる

上の例では、30-1=29

四分位範囲は\( 第3四分位数 ー 第1四分位数 \)で求められる。

第1四分位数と第3四分位数は、中央値を境に、下位グループと上位グループに分割し、それぞれのグループの中央値を指す。

ひげの長さは、上が「第3四分位数+1.5×四分位範囲」。下が「第1四分位数-1.5×四分位範囲」